En este artículo encontrarás toda la información necesaria respecto al uso de inferencia estadística y cálculo de probabilidad con el lenguaje R; todo ello con un enfoque práctico en vez de teórico, explicado de manera simple, y cubriendo el mayor número de casos posibles:
-
Inferencia Estadística
- A) Inferencia Sobre La Varianza
- B) Inferencia Sobre El Cociente De Varianzas
- D) Inferencia Sobre La Media Con Varianza Poblacional Conocida
- D) Inferencia Sobre La Media Con Varianza Poblacional Desconocida
- E) Inferencia Sobre La Diferencia De Medias Con Muestras Dependientes
- F) Inferencia Sobre La Diferencia De Medias Con Muestras Independientes
- G) Inferencia Sobre La Proporción
- H) Inferencia Sobre La Diferencia De Proporciones
- Distribuciones de Probabilidad
Inferencia Estadística
La inferencia estadística tiene como objetivo estudiar el comportamiento del conjunto de elementos sobre los que se investiga, con el fin de obtener conclusiones e informaciones numéricas útiles mediante las cuales hacer deducciones. Las principales herramientas de esta rama de la estadística son los intervalos de confianza y los contrastes de hipótesis.
Antes que nada, importaremos en R los datos del siguiente archivo csv que utilizaremos como ejemplo para cada apartado:
cepa <- read.csv(url("https://forodatos.com/multimedia/datos/notas-cepa.csv")) # Asignamos los datos a la variable cepa.
attach(cepa) # Usamos attach() para acceder con mayor facilidad al contenido de las variables.A) Inferencia Sobre La Varianza
En este caso debemos analizar si el valor de la varianza poblacional (σ^2) es estadísticamente distinto a un valor predefinido. Supongamos que queremos hacer inferencia sobre el parámetro de la varianza poblacional para la variable edad del archivo importado:
Ejemplo -> Calcular un intervalo al 90% de confianza para este parámetro:
# Hipótesis nula -> la varianza poblacional es estadísticamente igual a la del valor predefinido.
# Hipótesis alternativa -> la varianza tiene una valor estadístico diferente al predefinido.
# Primero hayamos los valores críticos para 0.90, que son 0.95 & 0.05:
qchisq(c(0.95, 0.05), # Valores críticos
df=29, # Grados de libertad
lower.tail=TRUE)
[1] 42.55697 17.70837 # Límites para la región de no rechazo
# Aplicamos la fórmula (n-1)*(sd()^2)/c(l1,l2):
(30-1)*(sd(edad)^2)/c(42.55697,17.70837)
[1] 184.3803 443.1050Al 90% de confianza el parámetro poblacional estará en el intervalo [184.38; 443.10]. Por lo tanto rechazamos la hipótesis nula y consideramos como factible la alternativa.
B) Inferencia Sobre El Cociente De Varianzas
Se utiliza para comprobar si las varianzas de dos muestras son similares o no.
Ejemplo -> Comparar las varianzas de las variables independientes X1er.trimestre & X3er.trimestre:
par(mfrow=c(1,2))
plot(X1er.trimestre,type="l")
plot(X3er.trimestre,type="l")
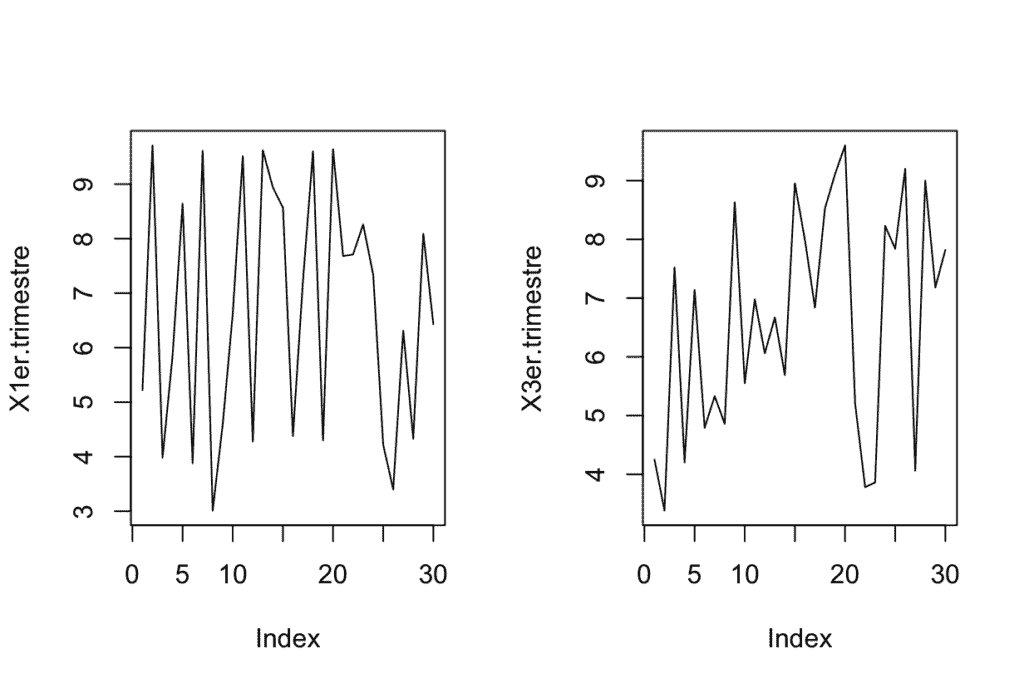
A simple vista observamos una mayor dispersión en la gráfica del primer trimestre, para obtener una certeza estadística sobre esta conclusión, haremos un test de diferencia de varianzas. Primero apilaremos las variables y posteriormente efectuaremos el contraste:
# Hipótesis nula -> hay igualdad de varianzas entre las 2 variables.
# Hipótesis alternativa -> la varianza es diferente para cada variable.
# Apilamos las variables:
apilados <- stack(cepa[, c("X1er.trimestre","X3er.trimestre")])
names(apilados) <- c("valor", "factor")
attach(apilados)
tapply(valor, factor, var)
# X1er.trimestre X3er.trimestre
# 5.052686 3.659173
# Efectuamos el contraste
var.test(valor ~ factor, alternative="two.sided", conf.level=.99, data=apilados)
F test to compare two variances
data:
valor by factor
F = 1.3808, num df = 29, denom df = 29, p-value = 0.805
alternative hypothesis: true ratio of variances is less than 1
99 percent confidence interval:
0.00000 3.34635
sample estimates:
ratio of variances
1.380827Obtenemos un valor F de 1.38 con un p-valor de 0.805, lo que indica que no hay evidencia suficiente para rechazar la hipótesis nula de igualdad de varianzas al 99% de confianza.
D) Inferencia Sobre La Media Con Varianza Poblacional Conocida
Ejemplo -> Determinar si la media de edad de la clase es igual que la de toda la escuela de adultos (μ = 37) para un 99% de confianza:
# Hipótesis nula -> la media de edad de la clase es igual que la de toda la escuela, es decir, 37 años.
# Hipótesis alternativa -> la media de edad es diferente de 37.
# Instalamos el paquete BSDA
install.packages("BSDA")
library("BSDA")
z.test(edad, alternative='two.sided',
mu=37, # Media de toda la escuela
sigma.x=17, # Desviación estándar de la variable edad
conf.level=.99) # 99% de confianza
One-sample z-Test
data: edad
z = 1.1814, p-value = 0.2375
alternative hypothesis: true mean is not equal to 37
99 percent confidence interval:
32.67191 48.66143
sample estimates
mean of x
40.66667 Con un p-valor de 0.2375, no hay evidencia suficiente para rechazar la hipótesis nula de que la media de edad es igual a 37 años al 99% de confianza.
D) Inferencia Sobre La Media Con Varianza Poblacional Desconocida
En este apartado analizaremos la edad de los estudiantes de una clase.
Ejemplo -> Determinar si la media de edad de la clase es igual que la de toda la escuela de adultos (μ = 37) para un 95% de confianza y omitiendo la varianza:
# Hipótesis nula -> la media de edad es igual a 37.
# Hipótesis alternativa -> la media de edad la clase no equivale a 37.
with(cepa, (t.test(edad,
alternative='two.sided',
mu=37,
conf.level=.95)))
One Sample t-test
data: edad
t = 1.2209,
df = 29, p-value = 0.2319
alternative hypothesis: true mean is not equal to 37
95 percent confidence interval:
34.52445 46.80888
sample estimates:
mean of x
40.66667 El intervalo de confianza es [34.52; 46.81], el cual incluye el valor 37. Por lo tanto, no hay evidencia suficiente para rechazar la hipótesis nula de que la media de edad es igual a 37 años.
E) Inferencia Sobre La Diferencia De Medias Con Muestras Dependientes
En este caso deseamos comprobar si influye de alguna manera que los alumnos tengan discapacidad reconocida (33%) en una mejora de calificaciones durante el curso.
Ejemplo -> Averiguar si hay una mejora en las calificaciones entre el primer y tercer trimestre (contando solo el primer decimal) para el 95% de confianza:
# Hipótesis nula -> la media de las notas del primer trimestre y las del tercero sone estadísticamente iguales.
# Hipótesis alternativa -> la media entre las dos variables es diferente de cero.
with(cepa, (t.test(X1er.trimestre, X3er.trimestre,
alternative='two.sided', conf.level=.95,
paired=TRUE))) # Muestras dependiente-apareada
Paired t-test
data: X1er.trimestre and X3er.trimestre
t = 0.15727, df = 29, p-value = 0.8761
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-1.076438 1.255771
sample estimates:
mean difference
0.08966667Obtenemos un intervalo de confianza de [-1.076438; 1.255771] en el cual está contenido el valor cero, por lo que consideraremos como factible la hipótesis nula.
F) Inferencia Sobre La Diferencia De Medias Con Muestras Independientes
Se utiliza para comprobar las diferencias estadísticas de una variable extraídas en muestras independientes diferencias por otra variable.
I) Varianzas Poblaciones Conocidas
Ejemplo -> Comparar las medias de las notas finales según el sexo para una confianza del 99%:
# Hipótesis nula -> la diferencia entre ambos géneros es estadísticamente equivalente
# Hipótesis alternativa -> la diferencia entre la media de hombres y mujeres es distinta de cero
# Aseguramos que esté importado el paquete BSDA
install.packages("BSDA")
library("BSDA")
# Creamos dos variables para la edad de los alumnos diferenciado por sexos (en este caso el dataset contiene una "idea feliz" con el mismo número de hombres y mujeres, si por ejemplo hubiese 17 mujeres y 13 hombres tendríamos que hacer edad_hombres|mujeres -> edad[sexo=="H|M"][1:13]
final_hombres <-final[sexo=="H"]
final_mujeres <-final[sexo=="M"]
z.test(final_hombres, final_mujeres, alternative='two.sided', sigma.x=sd(final_hombres), sigma.y=sd(final_mujeres), conf.level=0.99)
Two-sample z-Test
data: final_hombres and final_mujeres
z = -1.0468, p-value = 0.2952
alternative hypothesis: true difference in means is not equal to 0
99 percent confidence interval:
-1.6149498 0.6816164
sample estimates:
mean of x mean of y
6.200000 6.666667
El intervalo para el 99% de confianza es [-1.6149498; 0.6816164] en el cual está contenido el valor cero, lo que indica que no hay una diferencia estadística entre la nota final de hombres y mujeres. No rechazamos la hipótesis nula, ya que no hay evidencia suficiente para afirmar que existe una diferencia estadística entre las medias de hombres y mujeres.
II) Varianzas Poblaciones Desconocidas
Ejemplo -> Comparar las medias de las notas finales según el sexo para una confianza del 99% (omitiendo la varianza):
# Hipótesis nula -> la diferencia entre ambos géneros es estadísticamente equivalente
# Hipótesis alternativa -> la diferencia entre la media de hombres y mujeres es distinta de cero
t.test(final~sexo,
alternative='two.sided', # Bilateral
conf.level=.99,
var.equal=TRUE, data = cepa) # Asumimos que las varianzas desconocidas son iguales
Two Sample t-test
data: final by sexo
t = -1.0468, df = 28, p-value = 0.3041
alternative hypothesis: true difference in means between group H and group M is not equal to 0
99 percent confidence interval:
-1.6985059 0.7651725
sample estimates:
mean in group H mean in group M
6.200000 6.666667 En este caso nos encontramos con un intervalo de confianza igual a [-1.6985059; 0.7651725], el cual también abarca el valor cero; lo que significa que la nota media de los hombre es estadísticamente similar a la de las mujeres y por lo tanto rechazaremos la hipótesis alternativa.
G) Inferencia Sobre La Proporción
Consiste en hacer inferencia sobre la proporción poblacional.
Ejemplo -> Contrastar si la proporción es estadísticamente diferente de π = 0.6 para el 90% de confianza mediante aproximación normal:
# Hipótesis nula -> π es igual 0.6
# Hipótesis alternativa -> π es distinto a 0.6
prop.test(rbind(xtabs(~ discapacidad)),
alternative='two.sided',
p=.6, conf.level=.90)
1-sample proportions test with continuity correction
data: rbind(xtabs(~discapacidad)), null probability 0.6
X-squared = 0.3125, df = 1, p-value = 0.5762
alternative hypothesis: true p is not equal to 0.6
90 percent confidence interval:
0.4998461 0.8028172
sample estimates:
p
0.6666667 Obtenemos un intervalo [0.50; 0.80] para el 90% de confianza que nos impide rechazar la hipótesis nula.
H) Inferencia Sobre La Diferencia De Proporciones
Se utiliza para determinar si dos proporciones distintas son estadísticamente iguales.
Ejemplo -> Efectuar un contraste sobre las proporciones sexo y discapacidad para un 99% de confianza:
# Hipótesis nula -> la diferencia entre la proporción de ambas variables es estadísticamente nula
# Hipótesis alternativa -> las proporciones de las variables son diferentes
prop.test(xtabs(~sexo+discapacidad), alternative='two.sided', conf.level=.99)
2-sample test for equality of proportions without continuity correction
data: xtabs(~sexo + discapacidad)
X-squared = 3.1554e-31, df = 1, p-value = 1
alternative hypothesis: two.sided
99 percent confidence interval:
-0.4433842 0.4433842
sample estimates:
prop 1 prop 2
0.6666667 0.6666667
Dado que el estadístico es similar en ambas variables y hemos obtenido el intervalo de confianza [-0.4433842; 0.4433842] consideraremos como factible la hipótesis nula.
Distribuciones de Probabilidad
Las distribuciones de probabilidad tiene como objetivo establecer toda la gama de resultados de un experimento junto a la posibilidad de que estos sucedan.
Distribuciones de Probabilidad Continuas
Describen las probabilidades de los «x» valores de una variable aleatoria, esta clase de de distribuciones tienen la peculiaridad de que se calculan las areas de distribución en vez de los puntos exactos.
A) Distribución Uniforme
Este tipo de distribuciones modelan un rango de valores con igual probabilidad. Supongamos que en el vecindario de uno de los alumnos de la escuela de adultos van a cortar el Internet en algún momento de entre las próximas 24 horas por causas de mantenimiento, sin especificar la hora. Durante ese periodo no podrá acceder a Google Classroom ni nada relacionado con el estudio, por lo que nos interesa saber la probabilidad de que corten la red a «x» hora.
Para ello utilizaremos la siguiente fórmula:
punif(c(x), # Valor(es) de la variable
min = y, # Mínimo
max = z, # Máximo
lower.tail = TRUE|FALSE) # Cola izquierda (TRUE) o derecha (FALSE)Caso 1 -> Calcular la probabilidad de que ocurra dentro de las primeras 3 horas posteriores al aviso [P(X ≤ 3)]:
punif(c(3), # Establecemos como valor 3
min = 0, # Minuto cero posterior al aviso
max = 24, # Máximo de tiempo previo corte
lower.tail = TRUE) # Utilizamos la cola izquierda ≤ ya que buscamos la probabilidad de que la hora sea menor o igual que 3 [P(X ≤ 3)]
[1] 0.125El resultado es 0.125, lo que significa que hay un 12.5% de probabilidad de que el Internet se corte durante las primeras 3 horas.
Caso 2 -> Calcular la probabilidad de que ocurra durante las últimas 7 horas previas a la finalización del periodo dado de 24 horas [P(X > 17)]:
punif(c(17), # Establecemos como valor 17 (24 h - 7 h)
min = 0, # Minuto cero posterior al aviso
max = 24, # Máximo de tiempo previo corte
lower.tail = FALSE) # Utilizamos la cola derecha > ya que buscamos la probabilidad de que la hora sea superior a 17 pero menor de 25 [P(X > 17)]
[1] 0.2916667El resultado nos indica que hay un ~29.2% de probabilidades de que se corte el Internet en algún momento de las últimas 7 horas.
Caso 3 -> Debido a problemas “inesperados” han cambiado el periodo de espera a 7 días, y de nuevo no han dado un horario -o posible intervalo- para organizarnos. Por motivos de productividad nos interesa saber la probabilidad de que el corte de red ocurra durante el fin de semana. Supongamos que el retraso entra en vigor el jueves, por lo que sábado y domingo corresponderían a los días 3 & 4 respectivamente; afortunadamente al tratarse de una distribución uniforme eso es irrelevante y simplemente consideraremos que la probabilidad de que ocurra durante el sábado o domingo sea P[(X > 5)]:
punif(c(5), # Establecemos como valor 5 (número de días entre lunes y viernes)
min = 0, # Día cero posterior al nuevo aviso
max = 7, # Máximo de días previo mantenimiento
lower.tail = FALSE) # Utilizamos la cola derecha > ya que buscamos la probabilidad de que el día sea después que el viernes (5) pero sea antes que el lunes (8) [P(X > 5)]
[1] 0.2857143Hay un ~28.6% de probabilidad de que ocurra durante el fin de semana.
Caso 4 -> Dado el contexto anterior, ¿cuál sería la probabilidad de que ocurriese entre semana [P(X ≤ 5)]?
# Método 1: usando de nuevo punif()
punif(c(5), # Establecemos como valor 5 (número de días entre lunes y viernes)
min = 0, # Día cero posterior al nuevo aviso
max = 7, # Máximo de días previo mantenimiento
lower.tail = TRUE) # Utilizamos la cola izquierda ≤ ya que buscamos la probabilidad de que ocurra durante los 5 primeros días[P(X ≤ 5)]
[1] 0.7142857
# Método 2: usando como base el caso 3 [(1-[P(X > 5)]) = P(X ≤ 5)]
1 - punif(c(5),
min = 0,
max = 7,
lower.tail = FALSE)
[1] 0.7142857La probabilidad de que el corte ocurra entre semana es del ~71.4%.
B) Distribución Exponencial
Estas distribuciones modelizan el intervalo de tiempo que transcurre entre dos sucesos. Supongamos que el tiempo promedio de mantenimiento es de 90 minutos. Antes que nada debemos tener en cuenta el parámetro de la exponencial (θ), que en este caso es 1/90, y la fórmula que utilizaremos en R para realizar los cálculos:
pexp(x, # Valor(es) de la variable
rate = y, # Parámetro de la exponencial
lower.tail = TRUE|FALSE) # Cola izquierda (TRUE) o derecha (FALSE)Caso 1 -> Calcular la probabilidad de que el mantenimiento dure como máximo 65 minutos [P(X ≤ 65)]:
pexp(65, # 65 minutos
rate = 1/90, # 1/λ;90 minutos => 1/90 = λ => 1/MEDIA
lower.tail = TRUE) # Utilizamos la cola izquierda ≤ ya que buscamos la probabilidad dure como mucho 65 minutos.
[1] 0.5143282La probabilidad de que dure un máximo de 65 minutos es del ~51.4%.
Caso 2 -> Calcular la probabilidad de que el mantenimiento dure más de 110 minutos [P(X > 110)]:
pexp(110, # 110 minutos
rate = 1/90, # 1/λ;90 => 1/90 = λ => 1/MEDIA
lower.tail = FALSE) # Utilizamos la cola derecha > ya que buscamos la probabilidad de que dure más de 110 minutos.
0.2945748La probabilidad de que el tiempo de mantenimiento de Internet supere los 110 minutos es del ~29.5%.
Caso 3 -> El proveedor de Internet contratado por el alumno dura una extraordinaria media de 160 días sin caerse. Si una vez acabado el mantenimiento ya lleva 150 días y aún no ha habido ningún fallo, ¿cuál será la probabilidad de que haya una caída en los siguientes 28 días? [P(150 < X < 178) / P(X > 150)] = [P(X < 178) – P(X < 150)] / P(X > 150):
pexp(c(178,150), # P(X < 178), P(X < 150)
rate=1/160, # 1/λ;160 => 1/160 = λ => 1/MEDIA
lower.tail = TRUE) # P(150 < X < 178)
[1] 0.6712639 0.6083944
pexp(150,
rate=1/160, # 1/λ;160 => 1/160 = λ => 1/MEDIA
lower.tail = FALSE) # P(X > 150)]
[1] 0.3916056
# Procedemos a calcular la probabilidad condicional -> [P(150 < X < 178) / P(X > 150)] = [P(X < 178) - P(X < 150)] / P(X > 150) => (0.6712639 - 0.6083944) / 0.3916056
[1] 0.1605429La probabilidad de que haya una caída en los siguientes 28 días es del ~16.1%.
Caso 4 -> Partiendo del planteamiento del caso anterior, ¿cuál será la probabilidad de que haya una caída en algún momento de los siguientes 323 días?
pexp(c(473,150), # P(X < 473), P(X < 150)
rate=1/160, # 1/λ;160 => 1/160 = λ => 1/MEDIA
lower.tail = TRUE) # P(150 < X < 473)
[1] 0.9479864 0.6083944
pexp(150,
rate=1/160, # 1/λ;160 => 1/160 = λ => 1/MEDIA
lower.tail = FALSE) # P(X > 150)]
[1] 0.3916056
# Procedemos a calcular la probabilidad condicional -> [P(150 < X < 178) / P(X > 150)] = [P(X < 73) - P(X < 150)] / P(X > 150) => (0.9479864 - 0.6083944) / 0.3916056
[1] 0.8671786En este caso, la probabilidad de que falle el Internet es del ~86.7%.
C) Distribución Normal
Se trata de la principal distribución de probabilidad en estadística, y para su cálculo necesitamos 2 parámetros: la media (μ) y la desviación estándar-típica (σ). Para realizar los casos de este apartado utilizaremos la variable «edad» del archivo .csv importado al inicio de este artículo. Primero veremos la formulas que utilizaremos y acto seguido calcularemos la media y la desviación estándar:
# Probabilidad en distribución normal
pnorm(x, # Valor(es) de la variable
mean = y, # Media
sd = z, # Desviación estándar típica
lower.tail = TRUE|FALSE) # Cola izquierda (TRUE) o derecha (FALSE)
# Gráfico de densidad
plot(density(x), # Densidad de la variable
col = "color", # Color de la línea
main = "texto") # Título
# Cuantil para la probabilidad
qnorm(x, # Número o vector de probabilidades
mean = y, # Media
sd = z, # Desviación estándar
lower.tail = TRUE|FALSE) # Cola izquierda (TRUE) o derecha (FALSE)
# Representación de cuantiles
low <- min(which(dens_cepa$x >= min(edad)))
high <- max(which(dens_cepa$x < qt[2]))
polygon(c(dens_cepa$x[c(low, low:high, high)]),
c(0, dens_cepa$y[low:high], 0),
col = "blue")
# Recordad adjuntar las variables con «attach(cepa)»
sd(edad) # Desviación estándar
[1] 16.44916
mean(edad) # Media
[1] 40.66667A continuación generaremos el gráfico de densidad, que servirá de utilidad para visualizar los casos prácticos que encontrarás en este apartado:
plot(density(edad), # Densidad de la variable edad, si no hubiésemos usado attach() sería density(cepa$edad)
col = "black", # Línea de color negro
main = "Edad de los Estudiantes") # Título de la gráfica
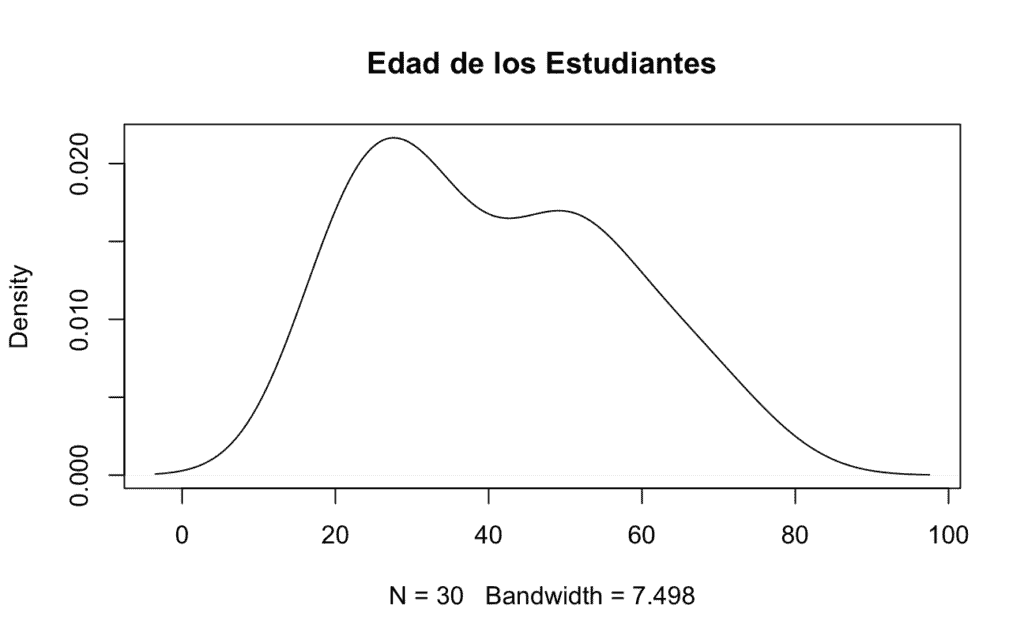
Vemos que la mayoría de alumnos se encuentran en unas edades comprendidas entre 20 y 60 años, el gráfico utiliza los datos de todos los alumnos (N = 30) y un ancho de banda de ~7.5 más que apropiado para aproximar la densidad que generan estos datos.
Caso 1 -> Calcular la probabilidad de que los alumnos tengan una edad comprendida entre 20 y 60 años. [P(20 ≤ X ≤ 60)] = 1 – [P(X ≤ 20) – P(X ≥ 60)]:
1 - pnorm(20, # P(X ≤ 20)
mean=mean(edad), # Media
sd=sd(edad), # Desviación estándar
lower.tail=TRUE) - # Buscamos la probabilidad de que sea menor o igual que 20.
pnorm(60, # P(X ≥ 60)
mean=mean(edad),
sd=sd(edad),
lower.tail=FALSE) # Buscamos la probabilidad de que sea mayor o igual que 60.
[1] 0.7755844Hay un 77.6% de probabilidad de que los alumnos tengan entre 20 y 60 años.
Caso 2 -> Calcular la probabilidad de que los alumnos estén en el intervalo de edades [18,30] | [P(18 ≤ X ≤ 30)] = 1 – [P(X ≤ 18) – P(X ≥ 30)]:
1 - pnorm(18, # P(X ≤ 18)
mean=mean(edad), # Media
sd=sd(edad), # Desviación estándar
lower.tail=TRUE) - # Buscamos la probabilidad de que sea menor o igual que 18.
pnorm(30, # P(X ≥ 30)
mean=mean(edad),
sd=sd(edad),
lower.tail=FALSE) # Buscamos la probabilidad de que sea mayor o igual que 30.
[1] 0.1742386La probabilidad de que los alumnos tengan entre 18 y 30 años es del ~17.4%.
Caso 3 -> Con el objetivo de que los alumnos se sientan más integrados, el jefe de estudios ha decidido reagrupar el aula en 3 grupos de edad. ¿En base a qué percentiles los debería reagrupar? ¿Entre qué rango de valores está comprendido cada grupo? Representa en la gráfica de densidad cada percentil.
Observando la gráfica al inicio de este apartado se deduce apropiado dividir el aula en los percentiles 0.2 & 0.7:
qnorm(c(0.2,0.7), # Cuantiles 0.2 & 0.7
mean=mean(edad), # Media edad
sd=sd(edad), # Desviación Estándar
lower.tail=TRUE) # Usamos el símbolo "menor o igual de" (≤)
[1] 26.82271 49.29261Dados estos resultados el primer grupo estaría formado por personas de 27 años para abajo, el segundo por edades comprendidas entre 27 y 49 y el tercero por alumnos mayores de 49 años. Una agrupación que resulta conveniente para que los alumnos se relacionen más entre ellos ya que, al ser de edades parecidas, se presume que tendrán mayor afinidad.
Por último, representaremos cada percentil en la gráfica de la función de densidad (recordad generarla de nuevo antes de introducir el código de abajo):
dens_cepa <- density(edad) # Asignamos la densidad de la columna edad a la variable dens_cepa
qt <- qnorm(c(0.2,0.7), mean=mean(edad), sd=sd(edad), lower.tail=TRUE) # Asignamos el cálculo de percentiles a la variable qt
# Representación del primer cuantil, en cada uno estableceremos los límites (mínimo y máximo) de coloreado
low <- min(which(dens_cepa$x >= min(edad))) # Mayor o igual que el valor mínimo de la variable edad
high <- max(which(dens_cepa$x < qt[2])) # Segundo valor obtenido en el cálculo de percentiles (49.29261)
polygon(c(dens_cepa$x[c(low, low:high, high)]),
c(0, dens_cepa$y[low:high], 0), # Pintamos el cuantil de color azul
col = "blue")
# Representación del segundo cuantil
low <- min(which(dens_cepa$x >= qt[1])) # Primer valor obtenido en el cálculo de percentiles (26.82271)
high <- max(which(dens_cepa$x < qt[2]))
polygon(c(dens_cepa$x[c(low, low:high, high)]),
c(0, dens_cepa$y[low:high], 0),
col = "orange")
# Representación del tercer cuantil
low <- min(which(dens_cepa$x >= qt[2]))
high <- max(which(dens_cepa$x < max(edad))) # Menor que el valor máximo de la variable edad
polygon(c(dens_cepa$x[c(low, low:high, high)]),
c(0, dens_cepa$y[low:high], 0),
col = "purple")
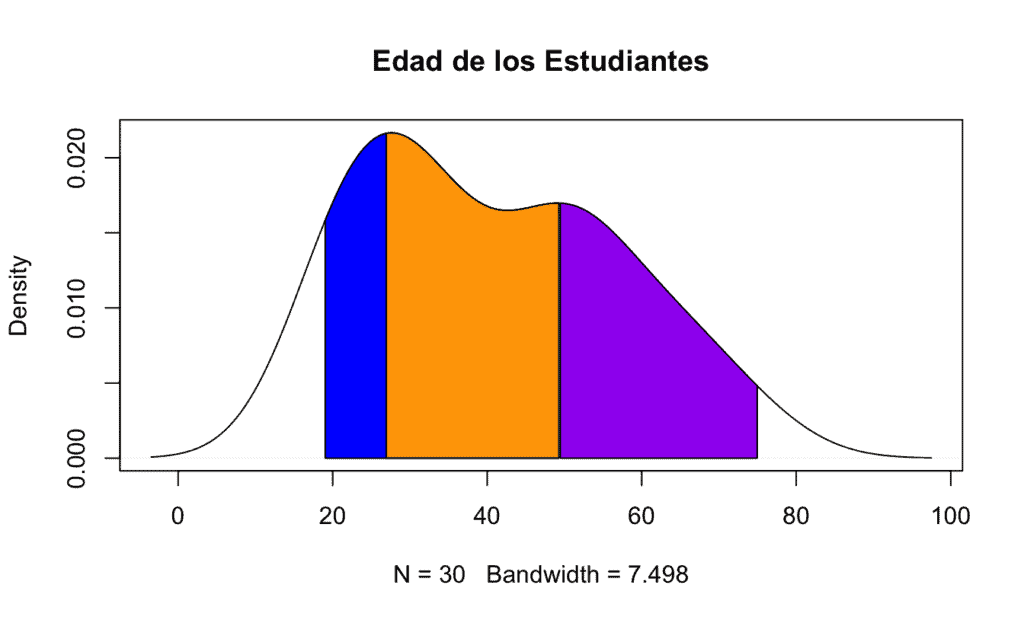
Caso 4 -> En un repentino cambio de planes, el jefe de estudios ha decidido finalmente reagrupar a los alumnos según la nota media del primer trimestre; con el objetivo de tener diferentes niveles para acomodar las clases a quienes no rinden lo suficiente. Antes de reorganizar a los alumnos debemos representar la gráfica de densidad de la variable «1er trimestre» y responder a lo siguiente: ¿Cuál es la probabilidad de que un alumno suspenda? ¿Qué probabilidad hay de que un alumno saque una media de calificaciones de entre 5 y 8? ¿Y un sobresaliente? ¿Y un 9.7? ¿Cuáles son los cuartiles de la distribución?
# I) Gráfica de la función de densidad:
plot(density(X1er.trimestre), # Densidad de la variable X1er.trimestre, si no hubiésemos usado attach() sería density(cepa$X1er.trimestre)
col = "black", # Línea de color negro
main = "Media del Primer Trimestre") # Título de la gráfica
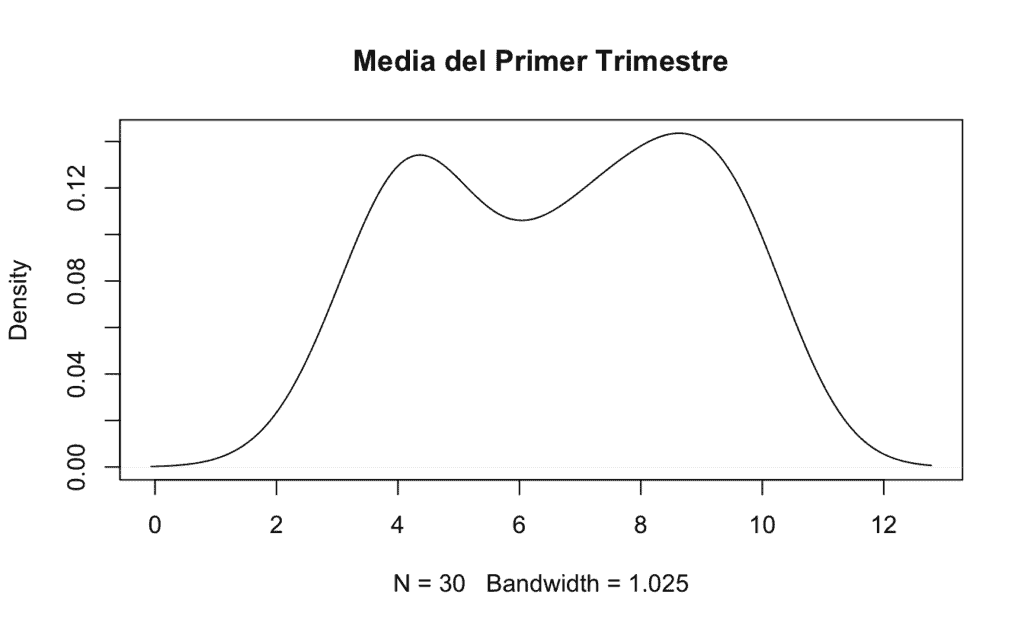 # Probabilidad de que un alumno suspenda [P(X ≤ 4.75)] (a partir del 4.75 se redondea a un 5):
pnorm(4.75, # Valor de la variable
mean = mean(X1er.trimestre), # Media
sd = sd(X1er.trimestre), # Desviación estándar típica
lower.tail = TRUE) # Cola izquierda
[1] 0.1930756 # La probabilidad de que un alumno suspenda es del ~19.3%.
# II) Probabilidad de que un alumno tenga una media comprendida entre 5 & 8 [P(5 ≤ X ≤ 8)]:
1 - pnorm(5, # P(X ≤ 5)
mean=mean(X1er.trimestre), # Media
sd=sd(X1er.trimestre), # Desviación estándar
lower.tail=TRUE) - # Buscamos la probabilidad de que sea menor o igual que 5.
pnorm(8, # P(X ≥ 8)
mean=mean(X1er.trimestre),
sd=sd(X1er.trimestre),
lower.tail=FALSE) # Buscamos la probabilidad de que sea mayor o igual que 8.
[1] 0.4937777 # La probabilidad de que saque entre un 5 y un 8 es del ~49.4%
# III) Probabilidad de que un alumno tenga una media superior al 8.75 [[P(X ≥ 8.75)]:
pnorm(8.75,
mean=mean(X1er.trimestre),
sd=sd(X1er.trimestre),
lower.tail = FALSE)
[1] 0.1806514 # La probabilidad de que un alumno supere el 8.75 de nota es del ~18.1%.
# IV) Probabilidad de que un alumno saque exactamente un 9.7 [[P(X = 9.7)]:
# La solución en estos casos es siempre cero. En las distribuciones de probabilidad continuas se calculan las áreas de distribución, no los puntos exactos.
# V) Cuartiles de la distribución [25%, 50%, 75%]:
qnorm(c(0.25,0.5,0.75),mean=mean(X1er.trimestre), sd=sd(X1er.trimestre), lower.tail = TRUE)
[1] 5.18187 6.69800 8.21413
# Probabilidad de que un alumno suspenda [P(X ≤ 4.75)] (a partir del 4.75 se redondea a un 5):
pnorm(4.75, # Valor de la variable
mean = mean(X1er.trimestre), # Media
sd = sd(X1er.trimestre), # Desviación estándar típica
lower.tail = TRUE) # Cola izquierda
[1] 0.1930756 # La probabilidad de que un alumno suspenda es del ~19.3%.
# II) Probabilidad de que un alumno tenga una media comprendida entre 5 & 8 [P(5 ≤ X ≤ 8)]:
1 - pnorm(5, # P(X ≤ 5)
mean=mean(X1er.trimestre), # Media
sd=sd(X1er.trimestre), # Desviación estándar
lower.tail=TRUE) - # Buscamos la probabilidad de que sea menor o igual que 5.
pnorm(8, # P(X ≥ 8)
mean=mean(X1er.trimestre),
sd=sd(X1er.trimestre),
lower.tail=FALSE) # Buscamos la probabilidad de que sea mayor o igual que 8.
[1] 0.4937777 # La probabilidad de que saque entre un 5 y un 8 es del ~49.4%
# III) Probabilidad de que un alumno tenga una media superior al 8.75 [[P(X ≥ 8.75)]:
pnorm(8.75,
mean=mean(X1er.trimestre),
sd=sd(X1er.trimestre),
lower.tail = FALSE)
[1] 0.1806514 # La probabilidad de que un alumno supere el 8.75 de nota es del ~18.1%.
# IV) Probabilidad de que un alumno saque exactamente un 9.7 [[P(X = 9.7)]:
# La solución en estos casos es siempre cero. En las distribuciones de probabilidad continuas se calculan las áreas de distribución, no los puntos exactos.
# V) Cuartiles de la distribución [25%, 50%, 75%]:
qnorm(c(0.25,0.5,0.75),mean=mean(X1er.trimestre), sd=sd(X1er.trimestre), lower.tail = TRUE)
[1] 5.18187 6.69800 8.21413 Por último, deberemos deducir los percentiles que consideremos más apropiados, especificar el rango de valores en los cuales está comprendido cada grupo y representar los cuantiles en la gráfica de densidad.
# En este caso dividiremos el aula en los percentiles 0.25 & 0.75
qnorm(c(0.25,0.75), mean=mean(X1er.trimestre), sd=sd(X1er.trimestre), lower.tail=TRUE)
[1] 5.18187 8.21413
# El primer grupo estará compuesto por alumnos con menos de un 5 de nota media, el segundo por estudiantes con notas de entre 5 y 8 puntos
y el tercero para quienes saquen más de un 8.
# Representar los cuantiles en la gráfica
dens_cepa <- density(X1er.trimestre) # densidad de la variable primer trimestre
qt <- qnorm(c(0.25,0.75), mean=mean(X1er.trimestre), sd=sd(X1er.trimestre), lower.tail=TRUE) # asignamos a qt el valor de los cuantiles
# Representación del primer cuantil
low <- min(which(dens_cepa$x >= min(X1er.trimestre))) # Mayor o igual que el mínimo de la variable X1er.trimestre
high <- max(which(dens_cepa$x < qt[2])) # Segundo valor obtenido al calcular los percentiles (8.21413)
polygon(c(dens_cepa$x[c(low, low:high, high)]),
c(0, dens_cepa$y[low:high], 0),
col = "blue")
# Representación del segundo cuantil
low <- min(which(dens_cepa$x >= qt[1])) # Primer valor obtenido después del cálculo de percentiles (5.18187)
high <- max(which(dens_cepa$x < qt[2]))
polygon(c(dens_cepa$x[c(low, low:high, high)]),
c(0, dens_cepa$y[low:high], 0),
col = "orange")
# Representación del tercer cuantil
low <- min(which(dens_cepa$x >= qt[2]))
high <- max(which(dens_cepa$x < max(X1er.trimestre))) # Establecemos como límite el valor máximo de la variable X1er.trimestre
polygon(c(dens_cepa$x[c(low, low:high, high)]),
c(0, dens_cepa$y[low:high], 0),
col = "purple")
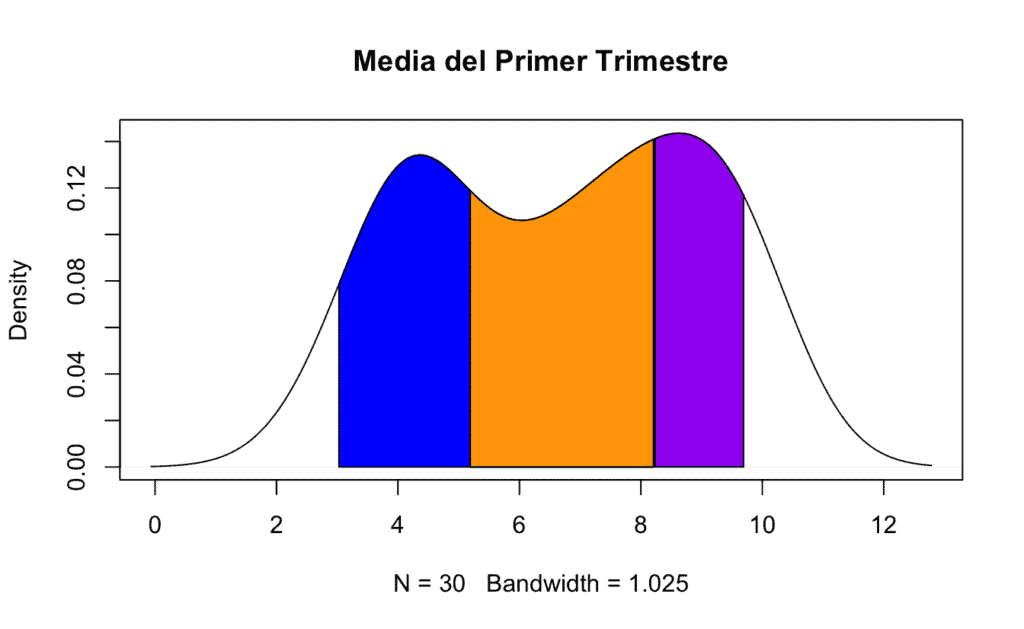
D) Distribución «T» de Student
Está asociada a la distribución normal y se suele utilizar cuando desconocemos la dispersión de la variable que queremos analizar. Utilizaremos la siguientes formulas:
pt(c(y), # «y» perteneciente a P(Y ≤|≥ y)
df=z, # df = grados de libertad (n-1)
lower.tail=TRUE|FALSE) # Cola izquierda (TRUE) o derecha (FALSE)
qt(c(.x), # cuantil(es) (0.6;0.7;0.8;0.9;...)
df=z # df = grados de libertad (n-1)
lower.tail=TRUE|FALSE) # ≤|>Caso 1 -> Calcular la probabilidad de que edad media de los alumnos sea inferior de 27 años, teniendo en cuenta que μ = 41 n = 30 y s = 16 [P(X̄ ≤ 27)]:
# Transformamos la variable X̄ en la variable Y promedio
y = (x - μ) / (s/sqrt(n)) = (27 - 41) / (16/sqrt(30)) # Fórmula para calcular «y» en R
[1] -4.792572
# Calculamos P(Y ≤ -4.792572)
pt(c(-4.792572), # «y» perteneciente a P(Y ≤ y)
df=29, # df = grados de libertad (n-1)
lower.tail=TRUE) # Usamos la cola izquierda ≤ ya que estamos buscando P(X̄ ≤ 27)
[1] 2.256953e-05 La probabilidad de que la media sea inferior de 27 años es del 0.002256953%.
Caso 2 -> Calcular la probabilidad de que la edad media de los alumnos sea superior de 58 años considerando los mismos parámetros que en el caso anterior. ¿Cuál es la puntuación «t» del cuantil 97 de esta distribución? [P(X̄ ≥ 58)]:
# Transformamos la variable X promedio en la variable Y promedio
y = (x - μ) / (s/sqrt(n)) = (58 - 41) / (16/sqrt(30)) # Calculamos de nuevo «y» en R, esta vez sustituyendo 27 por 58
[1] 5.819552
# Calculamos P(Y ≥ 5.819552)
pt(c(5.819552), # «y» perteneciente a P(Y ≥ y)
df=29, # df = grados de libertad (n-1)
lower.tail=FALSE) # Usamos la cola derecha ≥ ya que estamos buscando Y mayor o igual que y
[1] 1.307995e-06 # La probabilidad es del 0.0001307995%.
# Calculamos la puntuación «t» del cuantil 97
qt(c(.97), # cuantil
df=29, # df = grados de libertad (30-1)
lower.tail=TRUE) # ≤
[1] 1.957293 # valor «t» | «t» valor | puntuación «t»Caso 3 -> Calcular la probabilidad de que la edad media de los alumnos esté comprendida entre 60 y 76 años, teniendo en cuenta los parámetros anteriores pero poniéndonos en el supuesto que se hayan incorporado 5 alumnos más en el aula (n = 35). ¿Cuál será la puntuación «t» del cuantil 30 de esta distribución? [P(60 ≤ X̄ ≤ 76)] = 1 – [P(X̄ ≤ 60) – P(X̄ ≥ 76)]:
# Transformamos la variable X promedio en la variable Y promedio para cada probabilidad
y1 = (x - μ) / (s/sqrt(n)) = (60 - 41) / (16/sqrt(35)) # Calculamos «y» perteneciente a P(Y ≤ 60)
[1] 7.025345
y2 = (x - μ) / (s/sqrt(n)) = (76 - 41) / (16/sqrt(35)) # Calculamos «y» perteneciente a P(Y ≥ 76)
[1] 12.94142
# Calculamos 1 - [P(Y ≤ 60) - P(Y ≥ 76)]
1 - pt(c(7.025345), # «y» perteneciente a P(Y ≥ y)
df=34, # df = grados de libertad (35-1)
lower.tail=TRUE) - # Usamos la cola izquierda ≤
pt(c(12.94142),
df=34,
lower.tail=FALSE)
[1] 2.07526e-08 # La probabilidad de que la media de edades esté en el intervalo [60,76] es del 0.00000207526%
# Puntuación «t» del cuantil 80 de la distribución
qt(c(.30), # cuantil
df=34, # df = grados de libertad (35-1)
lower.tail=TRUE) # ≤
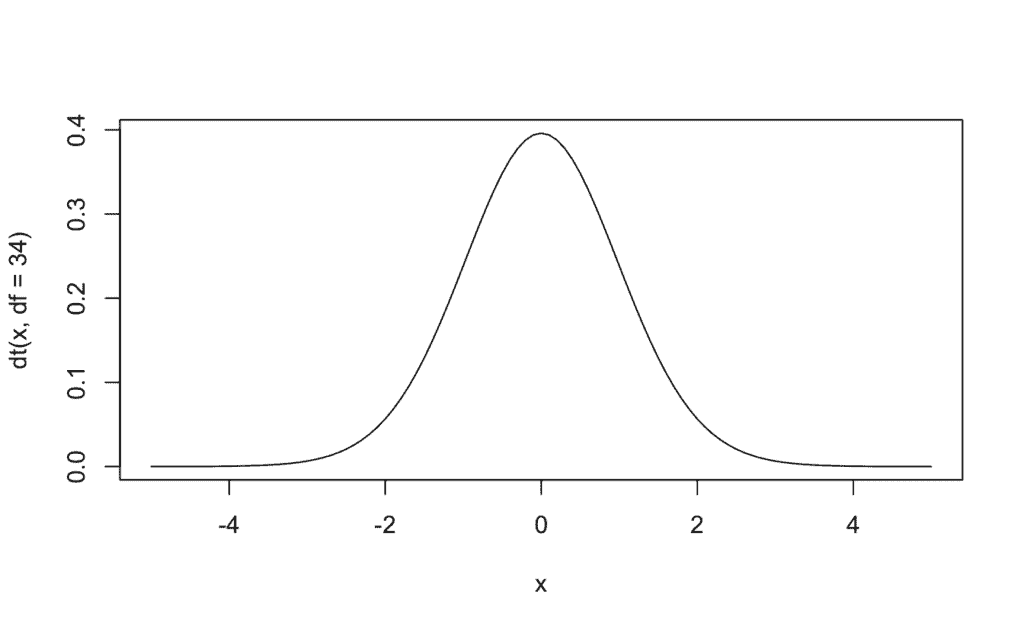
[1] -0.523212 # valor «t» | «t» valor | puntuación «t»Caso 4 -> Generar una gráfica de densidad para una distribución «t» con 34 grados de libertad y representar tres cuantiles a nuestra libre elección junto al calculado en el caso anterior:
# Generamos la gráfica de densidad
curve(dt(x, df=34), from=-5, to=5) # [-5,5] aproximado mediante el calculo del cuantil 0.00001
 # Calculamos los cuantiles (en este caso 0.14, 0.3, 0.56, 0.85)
qt(c(.14,.3,.56,.85), # cuantil - .3 similar al calculado en el anterior caso
df=34, # df = grados de libertad (35-1)
lower.tail=TRUE) # ≤
[1] -1.0978135 -0.5293532 0.1521090 1.0524849
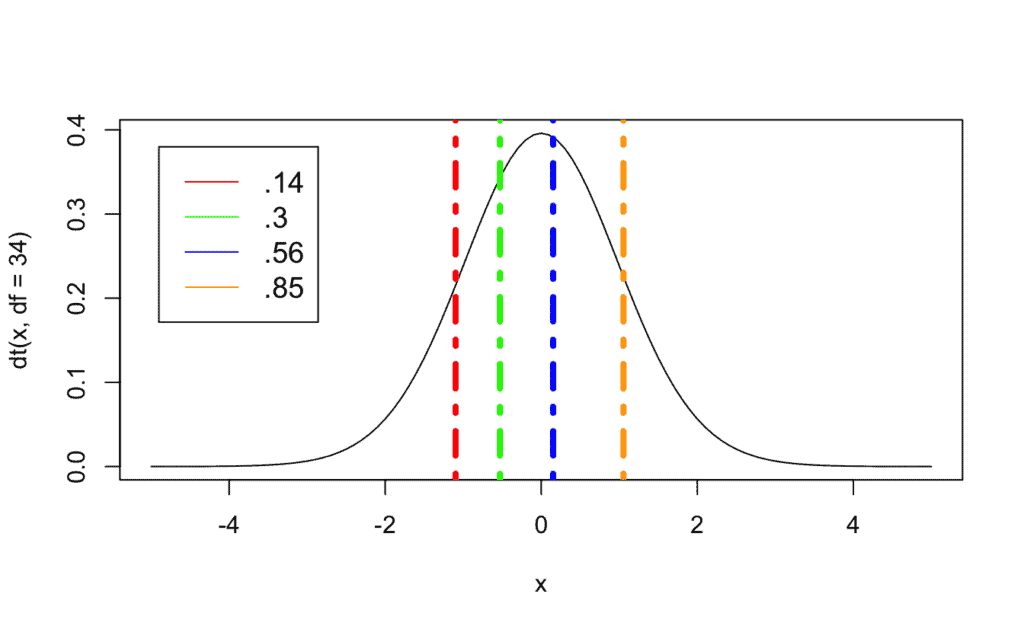
# Representamos los cuatro cuantiles (recordad generar la gráfica antes de ejecutar el código)
abline(v = c(-1.0978135, -0.5293532, 0.1521090, 1.0524849),
col = c("red","green","blue","orange"),
lwd = 4, lty = 4) # Línea vertical discontinua
# Añadimos una leyenda para interpretar la gráfica con mayor facilidad
legend(-4.9, .38, # Posición respecto a x,y
legend=c(".14", ".3", ".56", ".85"),
col=c("red", "green", "blue", "orange"),
lty=1, cex=1.2)
# Calculamos los cuantiles (en este caso 0.14, 0.3, 0.56, 0.85)
qt(c(.14,.3,.56,.85), # cuantil - .3 similar al calculado en el anterior caso
df=34, # df = grados de libertad (35-1)
lower.tail=TRUE) # ≤
[1] -1.0978135 -0.5293532 0.1521090 1.0524849
# Representamos los cuatro cuantiles (recordad generar la gráfica antes de ejecutar el código)
abline(v = c(-1.0978135, -0.5293532, 0.1521090, 1.0524849),
col = c("red","green","blue","orange"),
lwd = 4, lty = 4) # Línea vertical discontinua
# Añadimos una leyenda para interpretar la gráfica con mayor facilidad
legend(-4.9, .38, # Posición respecto a x,y
legend=c(".14", ".3", ".56", ".85"),
col=c("red", "green", "blue", "orange"),
lty=1, cex=1.2)
Distribuciones de Probabilidad Discretas
Estas distribuciones de probabilidad especifica todos los valores posibles de una variable junto con la factibilidad de que cada uno suceda.
A) Distribución Binomial
Mide la probabilidad de éxito para cada ensayo en una secuencia determinada. Supongamos que la probabilidad de que un alumno falte un día a clase es del 6.5% [p = 0.065]:
Caso 1 -> ¿Cuál es la probabilidad de que falte a clase una semana entera P(X = 5)? Representa gráficamente la masa de probabilidad:
table <- data.frame(Pr=dbinom(0:5,
size=5, # Número de días
prob=0.065)) # 6.5%
rownames(table) <- 0:5
table # Mostramos la tabla
0 0.714591842834 # Probabilidad de que no falte a clase ningún día [P(X = 0)]
1 0.248387538953
2 0.034535165844
3 0.002400840406
4 0.000083451672
5 0.000001160291 # P(X = 5)
# Representamos la masa de probabilidad
plot(0:5, dbinom(0:5, size=5, prob=0.065),type='h') # 'h'
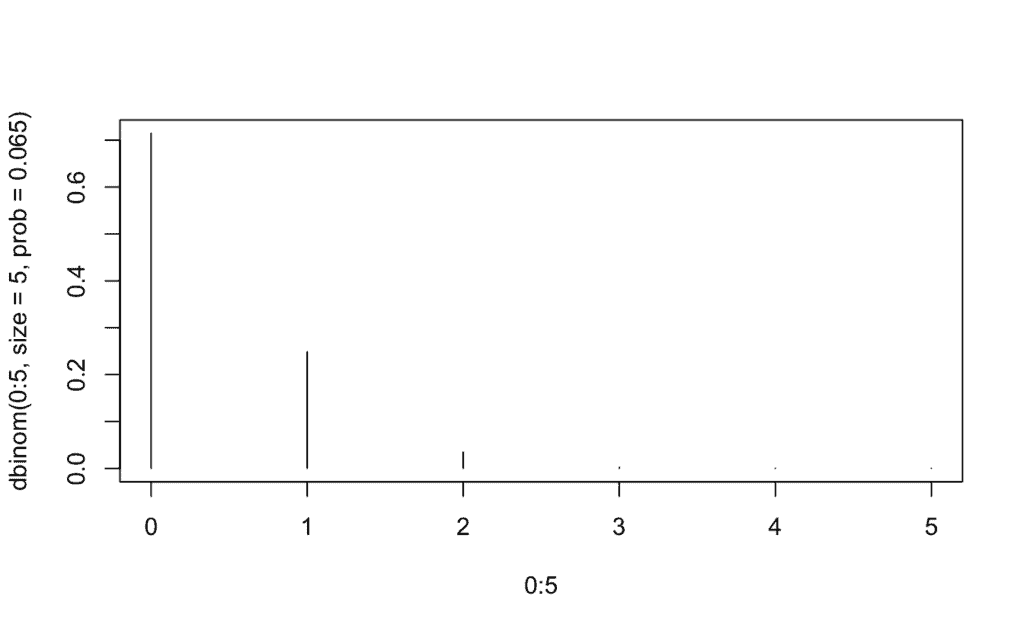
La probabilidad de que un alumno falte durante una semana entera es del 1.160291 × 10-6 por ciento.
Caso 2-> ¿Cuál es la probabilidad de que falte a clase un mes entero P(X = 20)? Representa gráficamente la probabilidad acumulada:
table <- data.frame(Pr=dbinom(0:20,
size=20,
prob=0.065))
rownames(table) <- 0:20 # Número de tablas
tail(table, n = 1) # Mostramos el último valor -20- de la tabla (expresado en notación científica)
20 1.812455e-24
# Representamos la probabilidad acumulada
plot(0:20, pbinom(0:20, size = 20, prob = 0.065), type="s")
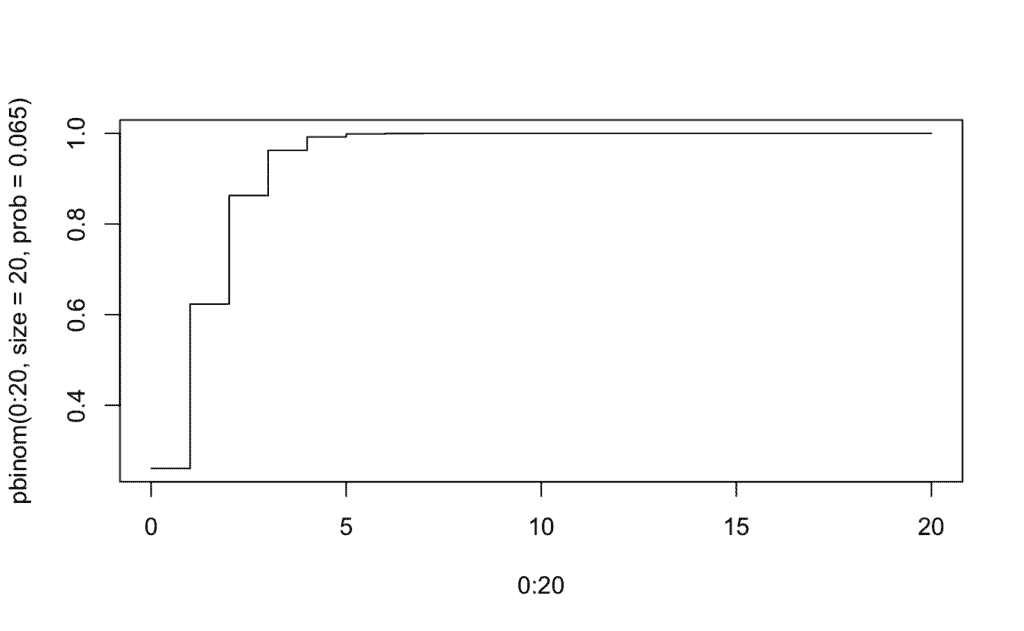
La probabilidad de que falte a clase durante un mes entero es del 1.812455e-24 por ciento, un valor prácticamente nulo.
Caso 3 -> Haz 10 ensayos binomiales equivalente a 2 semanas lectivas para un hipotético p = 0.25. ¿Cuál es la probabilidad de que un alumno falte a clase durante más de 8 días [P(X ≥ 8)]? ¿Y entre 3 y 7 días [P(3 ≤ X ≤ 7)]? ¿Y durante menos de 2 [P(X ≤ 2)]? Representa gráficamente la probabilidad acumulada y también cada intervalo de probabilidad:
# P(X ≥ 8)
pbinom(c(0:10), size=10, prob=0.25, lower.tail = FALSE)
# Resultados formateados manualmente
[0] 0.9436864852905
[1] 0.7559747695923
[2] 0.4744071960449
[3] 0.2241249084473
[4] 0.0781269073486
[5] 0.0197277069092
[6] 0.0035057067871
[7] 0.0004158020020
[8] 0.0000295639038 # P(X ≥ 8) | La probabilidad es del 0.002%
[9] 0.0000009536743
[10] 0.0000000000000
# P(3 ≤ X ≤ 7) => 1 - P(3 ≤ X) - P(7 ≥ X)
1 - pbinom(c(3),
size = 10,
prob = 0.25, lower.tail = TRUE) -
pbinom(c(7),
size = 10,
prob 0.25, lower.tail = FALSE)
[1] 0.2237091
# P(X ≤ 2)
pbinom(c(0:10), size=10, prob=0.25, lower.tail = TRUE)
# Resultados formateados manualmente
[0] 0.05631351
[1] 0.24402523
[2] 0.52559280 # P(X ≤ 2) | La probabilidad de que falte a clase durante menos de 2 días es del 52%
[3] 0.77587509
[4] 0.92187309
[5] 0.98027229
[6] 0.99649429
[7] 0.99958420
[8] 0.99997044
[9] 0.99999905
[10] 1.00000000
# Probabilidad acumulada
plot(0:10, pbinom(0:10, size = 10, prob = 0.25), type="s")
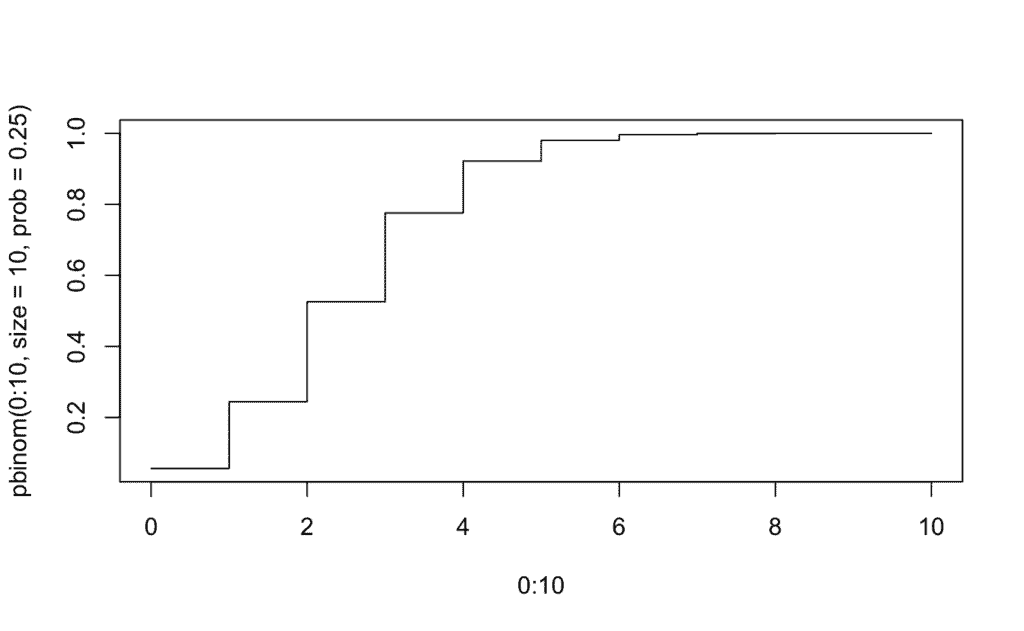
Por último, procedemos a representamos gráficamente cada intervalo de probabilidad; para ello generaremos la gráfica de la función de masa probabilística y colorearemos cada segmento:
plot(0:10, dbinom(0:10, size=10, # Número de ensayos
prob=0.25),type='h', # p = 0.25
col=c(rep("red",3), # Color rojo para P(X ≤ 2) | 3 <-> [0,2)
rep("purple",5), # Color morado para P(3 ≤ X ≤ 7) | 8 <-> (3,8)
rep("orange",3))) # Color naranja P(X ≥ 8) | 8 <-> (8,10]
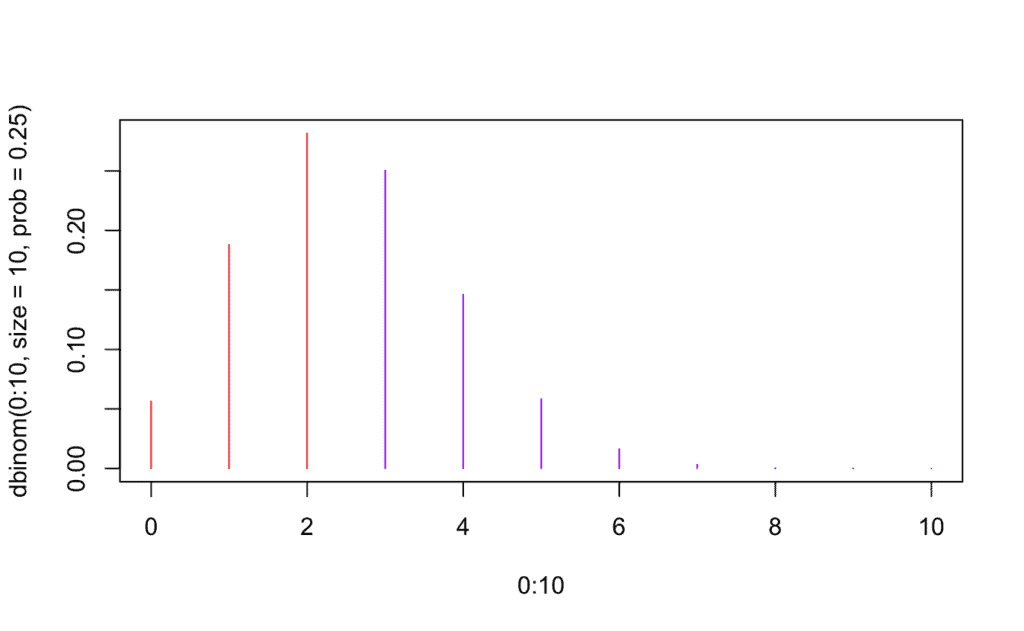
B) Distribución Geométrica
Está asociada a la distribución binomial y describe la probabilidad del número de ensayos necesarios para obtener un «éxito». Supongamos que la últimas 3 semanas de clase son de asistencia voluntaria y de utilidad para afianzar conocimientos y prepararse para posibles exámenes de recuperación. Con una probabilidad de asistencia del 17.5% [p = 0.175]:
Caso 1 -> Calcular la probabilidad de un alumno vaya a clase en algún día de la primera semana [P(X ≤ 5) => P(Y ≤ 5)]:
pgeom(c(4), # n-1 = 5-1 = 4
prob=0.175, # 17.5%
lower.tail=TRUE) # ≤
[1] 0.6178184La probabilidad de que vaya a clase en este caso es del ~61.8%.
Caso 2 -> Calcular la probabilidad de que un alumno asista a clase algún día comprendido entre el miércoles de la primera semana y el lunes de la tercera semana [P(3 ≤ X ≤ 11)].
1 - pgeom(c(2), # n-1 = 3-1 = 2
prob=0.175, # 17.5%
lower.tail=TRUE) - # ≤
pgeom(c(10), # 11-1 = 11-1 = 10
prob=0.175, # 17.5%
lower.tail=FALSE) # ≤
[1] 0.4410139Hay un 44.1% de probabilidad de que vaya a clase algún día entre el día 3 y el día 11.
Caso 3 -> ¿Cuál es la probabilidad de que un alumno asista a clase durante algún día de entre las 3 semanas [P(X ≤ 15) => P(Y ≤ 15)]? Representa la gráfica de la distribución geométrica:
# P(Y <=15) donde Y es el número de días hasta el primer éxito
pgeom(14, prob=0.175, lower.tail=TRUE) # P(X <=14)
[1] 0.9441775
# En este caso la probabilidad es del 94.4%
# La probabilidad de que un alumno asista a clase en algún día de los primeros 15 días es del 94.4%.
plot(0:15, dgeom(c(0:15), prob=0.175),type='h')
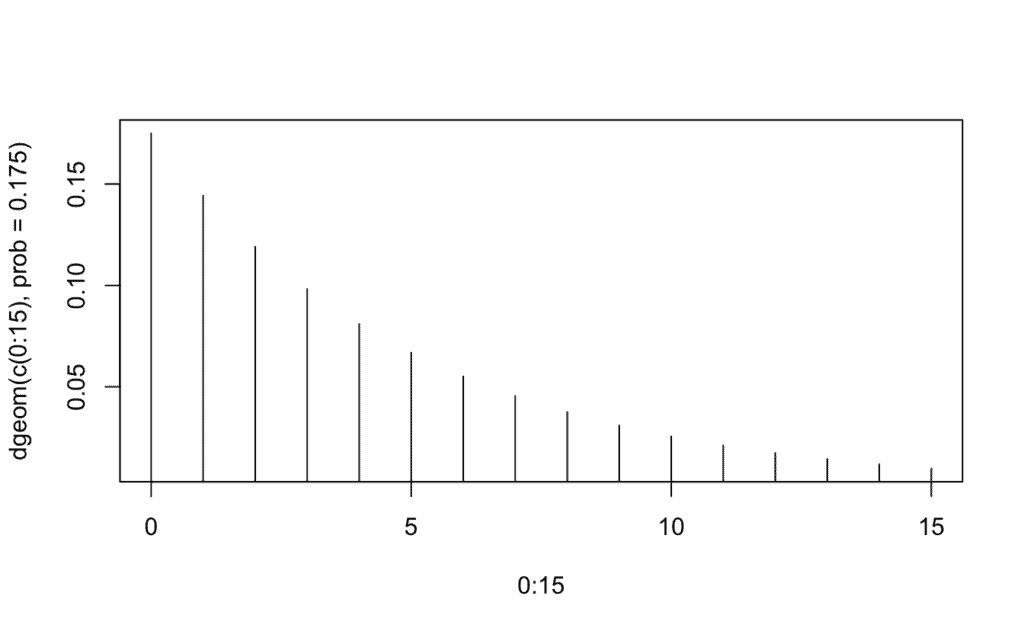 # La probabilidad va disminuyendo a medida que aumenta el número de días
# La probabilidad va disminuyendo a medida que aumenta el número de díasC) Distribución Hipergeométrica
Se utiliza en muestreos aleatorios en los cuales no se devuelve el elemento extraído. Supongamos que para la recuperación de matemáticas un alumno ha estudiado 16 de los 21 temas que hay en el libro:
Caso 1 -> Si en el examen cae el contenido de 13 temas elegidos aleatoriamente, ¿cuál es la probabilidad de que el alumno haya estudiado exactamente dichos temas [N1 = 16 | N2 = 5 | N = 21]? ¿Y la probabilidad más alta?
table <- data.frame(Pr=dhyper(0:13, # Tamaño de la muestraa
m = 16, # N1
n = 5, # N2
k = 13)) # 13 temas aleatorios
rownames(table) <- 0:13
table
[0] 0.000000000
[1] 0.000000000
[2] 0.000000000
[3] 0.000000000
[4] 0.000000000
[5] 0.000000000
[6] 0.000000000
[7] 0.000000000
[8] 0.063246351
[9] 0.281094894
[10] 0.393532852
[11] 0.214654283
[12] 0.044719642
[13] 0.002751978La probabilidad de que haya estudiado los 13 temas es del ~0.28%. Mientras que la probabilidad más alta es P(X = 10) = 0.393532852, es decir, una factibilidad del 39.3% de que haya estudiado 10 de los 13 temas del examen.
Caso 2 -> Partiendo del caso anterior, ¿cuál será la probabilidad de que sepa al menos 7 de los 13 temas [P(X ≥ 7)]? ¿Y menos de 11 temas [P(X ≤ 11)]? Representa la masa de probabilidad y la probabilidad acumulada de esta distribución.
# [P(X ≥ 7)]
phyper(c(6), # En este caso R lo interpretaría como [P(X > 7)] por lo que deberemos hacer x -1 => [P(X ≥ 7)] = [P(X > 6)]
m=16, n=5, k=13, lower.tail=FALSE)
[1] 0.9525284 # Hay un 95.25% de probabilidad de que sepa como mínimo 7 de los 13 temas.
# [P(X ≤ 11)]
phyper(c(11), # P(X ≤ 11)
m=16, n=5, k=13, lower.tail=TRUE)
[1] 0.9525284 # Hay un 95.25% de probabilidad de que el alumno sepa como mucho 11 temas de los 13 que caerán en el examen.Por último, representamos la función de masa probabilística y la probabilidad acumulada:
# Masa de probabilidad
plot(0:13, dhyper(0:13, m=16, n=5, k=13),type='h') # 'h'
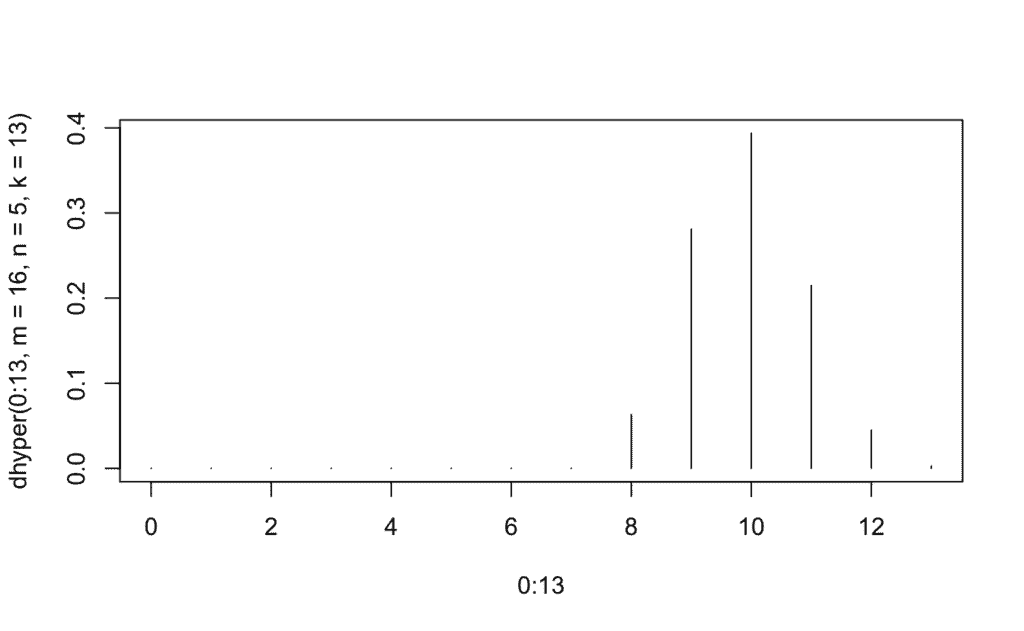 # Probabilidad acumulada
plot(0:13, phyper(0:13, m=16, n=5, k=13), type="s")
# Probabilidad acumulada
plot(0:13, phyper(0:13, m=16, n=5, k=13), type="s")
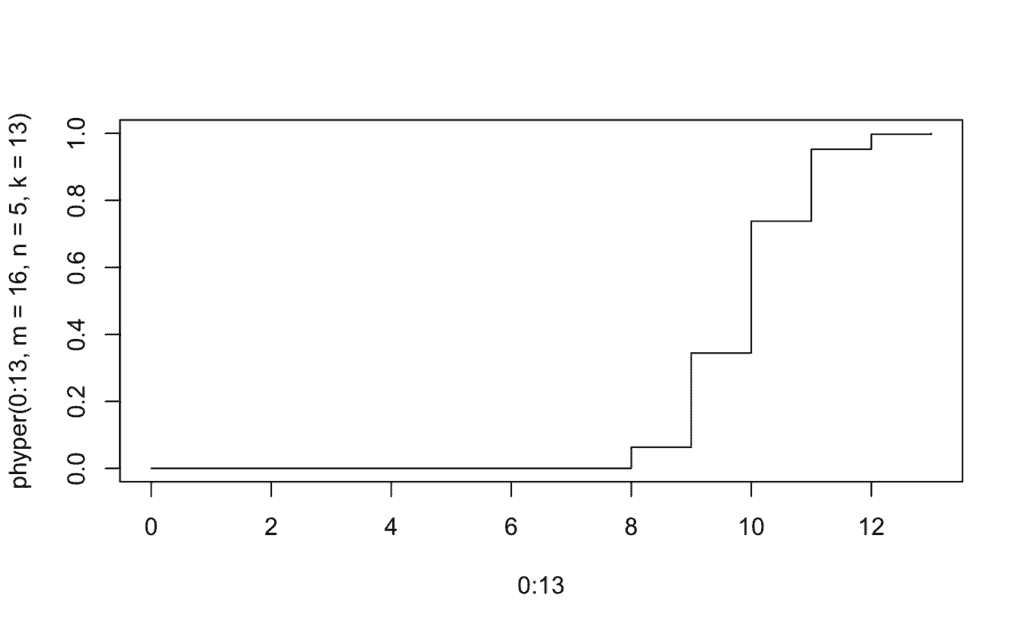
D) Distribución De Poisson
En esta distribución se calcula la probabilidad de que ocurra cierto evento en un periodo determinado a partir de una frecuencia de ocurrencia media lambda (λ). Supongamos que el tiempo media de espera hasta que un profesor llega a clase es de 4 minutos (λ = 4):
Caso 1 -> ¿Cuál es la probabilidad de que tarde 10 minutos en llegar [P(X = 10)]?
dpois(10, lambda = 4)
[1] 0.005292477La probabilidad es del 0.5%.
Caso 2 -> ¿Cuál es la probabilidad de que solamente tarde un minuto en llegar [P(X = 1)] ?
dpois(1, lambda = 4)
[1] 0.07326256La probabilidad de que tarde un minuto es del 7%.
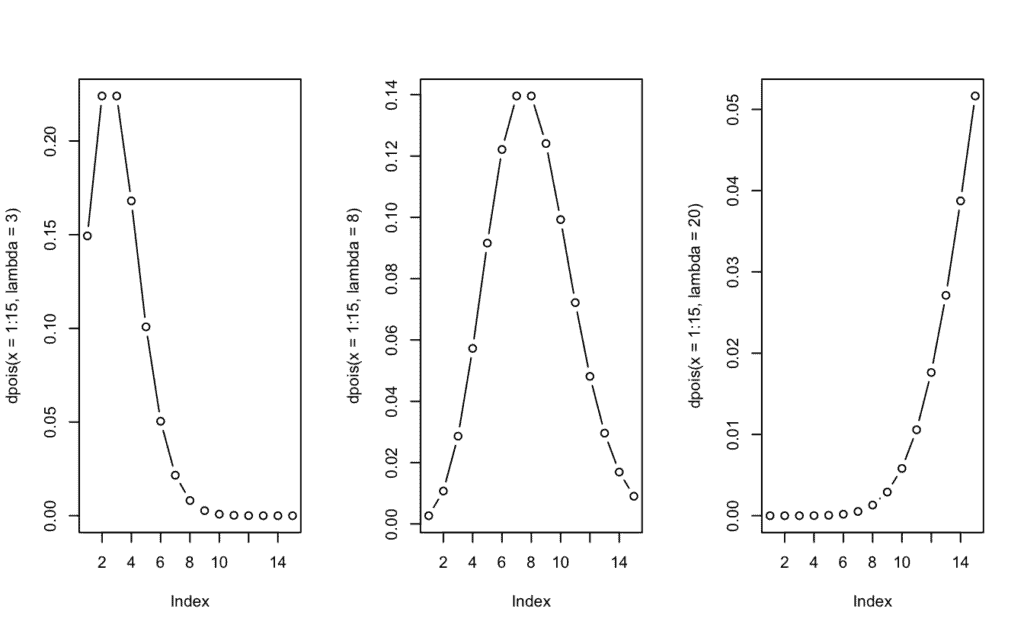
Caso 3 -> Calcula la probabilidad de que tarde 15 minutos para λ = 3, 8 y 20. Representa gráficamente la distribución para cada parámetro.
dpois(15, lambda = c(3,8,20))
[1] 0.0000005463057 0.0090259794111 0.0516488535318
# Las probabilidades son aproximadamente 0.00005%, 0.9026% y 5.16% respectivamente.
# Representamos individualmente la distribución Poissoniana para cada valor de lambda
par(mfrow=c(1,3)) # 1 fila con 3 gráficos
plot(dpois(x=1:15,
lambda=3), # λ = 3
type="b") # Gráfico de líneas y puntos
plot(dpois(x=1:15,lambda=8),type="b")
plot(dpois(x=1:15,lambda=20),type="b")