El ruido aditivo es un concepto fundamental que impacta directamente los resultados de modelos y técnicas algorítmicas en ciencia de datos y aprendizaje automático. Este artículo profundiza en qué es exactamente este fenómeno, cómo se manifiesta en distintos contextos y las estrategias más efectivas para controlarlo, especialmente en áreas donde la precisión resulta crítica como el procesamiento de imágenes, señales y datos de sensores.
- Definición y Características del Ruido Aditivo
- Tipos de Ruido Aditivo
- Impacto del Ruido Aditivo en Machine Learning
- Ejemplos Prácticos de Ruido Aditivo
- Métodos de Mitigación del Ruido Aditivo
- Aplicaciones Avanzadas
- Conclusión
Definición y Características del Ruido Aditivo
El ruido aditivo constituye una forma de perturbación que se suma directamente a una señal original. Desde una perspectiva matemática, podemos expresarlo mediante la ecuación:
$y(t) = x(t) + n(t)$
Donde:
- $y(t)$ representa la señal observada (con ruido)
- $x(t)$ corresponde a la señal original (sin ruido)
- $n(t)$ es el ruido aditivo propiamente dicho
Este tipo de ruido puede originarse por múltiples factores, incluyendo el entorno físico (como el ruido térmico en sistemas eléctricos), errores de medición, o imperfecciones en dispositivos de captura de datos. Por su amplia presencia en sistemas reales, el ruido aditivo se ha convertido en un modelo efectivo y relativamente simple para representar perturbaciones en diversos contextos.
Las características distintivas del ruido aditivo incluyen:
- Aleatoriedad: se comporta de manera impredecible, aunque puede seguir distribuciones estadísticas conocidas como la normal o gaussiana.
- Aditividad: se suma directamente a la señal original, diferenciándose así de otros tipos de interferencias que podrían aplicarse de forma multiplicativa o no lineal.
- Distribución Estadística: frecuentemente sigue patrones estadísticos reconocibles, siendo la distribución gaussiana uno de los más comunes.
- No Informativo: no contiene información útil para el análisis o procesamiento de señales, degradando invariablemente la calidad de los datos.
Tipos de Ruido Aditivo
El campo del procesamiento de señales y ciencia de datos distingue varios modelos de ruido aditivo, cada uno con propiedades y aplicaciones específicas:
1. Ruido Aditivo Blanco Gaussiano (AWGN)
Este tipo de ruido sigue una distribución normal o gaussiana, con media cero y desviación estándar constante. Es completamente aleatorio y carece de correlación con la señal original. El término “blanco” indica su distribución espectral uniforme a través de todas las frecuencias, similar a cómo la luz blanca contiene todas las frecuencias del espectro visible.
Las propiedades fundamentales del AWGN incluyen:
- Media cero: el valor promedio del ruido es cero, lo que evita introducir sesgos sistemáticos en la señal.
- Varianza constante: la dispersión de los valores alrededor de la media permanece constante, implicando que la intensidad del ruido no varía con el tiempo o la frecuencia.
- No correlacionado: cada muestra de ruido es estadísticamente independiente de las demás, por lo que conocer un valor no proporciona información sobre otros valores.
El AWGN es un modelo fundamental en teoría de la información, usado ampliamente para imitar el efecto de muchos procesos aleatorios naturales[5]. Este modelo resulta particularmente útil en procesamiento de señales, telemetría y comunicaciones digitales, donde uno de los mayores desafíos consiste en diseñar sistemas robustos frente a este tipo de interferencia.
2. Ruido Aditivo Laplaciano
Este tipo de ruido sigue una distribución de Laplace, caracterizada por una forma de doble exponencial. En comparación con el ruido gaussiano, presenta colas más largas, lo que aumenta la probabilidad de valores extremos.
Sus características principales son:
- Colas largas: la distribución laplaciana tiene colas más gruesas que la gaussiana, incrementando la probabilidad de valores extremos o atípicos.
- Media cero: al igual que el ruido gaussiano, su media es cero, evitando introducir sesgos en los datos.
- Impulsividad: genera valores atípicos o picos con mayor probabilidad que el ruido gaussiano, lo cual puede resultar problemático en ciertos modelos.
Este tipo de ruido resulta particularmente útil para modelar fenómenos donde ocurren cambios bruscos o saltos repentinos en los datos, siendo menos común que el AWGN pero relevante en ciertos tipos de procesamiento de imágenes y problemas de optimización en machine learning.
3. Ruido Aditivo Uniforme
Este ruido presenta una distribución uniforme, donde cualquier valor dentro de un rango específico tiene exactamente la misma probabilidad de ocurrir. Es común en simulaciones de entornos controlados o en modelos donde se requiere introducir incertidumbre de manera equilibrada.
Sus propiedades características incluyen:
- Distribución plana: todos los valores dentro del rango especificado tienen idéntica probabilidad de ocurrencia.
- Rango acotado: el ruido está estrictamente limitado a un intervalo definido (por ejemplo, entre -a y a), sin valores fuera de ese rango.
- Independencia entre muestras: cada muestra generada es independiente de las demás, sin correlaciones entre ellas.
Este tipo de ruido es particularmente útil en simulaciones y modelos digitales donde se necesita modelar incertidumbre acotada o errores controlados.
4. Ruido Aditivo de Cuantización
Este ruido surge específicamente durante la conversión de señales analógicas a digitales. Al reducir el número de bits que representan una señal continua, se introduce inevitablemente un error de cuantización, que puede modelarse como ruido aditivo.
Sus características distintivas son:
- Error discreto: surge debido a la diferencia entre el valor analógico real y su representación digital más cercana.
- Distribución uniforme: en sistemas ideales, el error sigue una distribución uniforme dentro del rango determinado por el tamaño del paso de cuantificación.
- Dependencia del número de bits: el nivel del ruido está directamente relacionado con el número de bits utilizados; a mayor cantidad de bits, menor será el error introducido por cuantización.
Este tipo de ruido es particularmente relevante en sistemas digitales como audio y video, donde las señales continuas deben discretizarse manteniendo la mayor calidad posible.
Impacto del Ruido Aditivo en Machine Learning
El ruido aditivo puede afectar significativamente el desempeño de los modelos de machine learning, particularmente en tareas de regresión y clasificación. La presencia de ruido en los datos de entrenamiento puede conducir a modelos menos precisos y aumentar el riesgo de sobreajuste si no se maneja adecuadamente.
1. En Modelos de Regresión
En los modelos de regresión, el ruido aditivo obstaculiza la capacidad del algoritmo para identificar la relación subyacente entre variables dependientes e independientes. Dado que el ruido se suma directamente a los valores reales de la variable dependiente, puede provocar que el modelo aprenda patrones incorrectos o distorsionados.
Por ejemplo, en un modelo de regresión lineal simple:
$y = \beta_0 + \beta_1 x + \epsilon$
Donde $\epsilon$ representa el término de error que incluye el ruido aditivo. Si el nivel de ruido es excesivo, el modelo perderá precisión y generará predicciones poco confiables.
2. En Clasificación
En problemas de clasificación, el ruido aditivo puede alterar tanto las características como las etiquetas de los datos, causando que los clasificadores produzcan predicciones erróneas. En el reconocimiento de imágenes, por ejemplo, el ruido aditivo puede hacer que elementos cruciales como objetos o bordes sean menos visibles para el modelo, reduciendo la precisión del clasificador.
3. Estrategias de Solución
Para mitigar los efectos negativos del ruido aditivo en modelos de machine learning, existen diversas estrategias:
- Filtrado de Datos: aplicar técnicas de filtrado para eliminar o reducir el ruido antes de entrenar los modelos. Entre los métodos más utilizados se encuentran el filtro de media móvil y el filtro de Kalman para señales temporales.
- Regularización: la regularización en modelos de machine learning, como la regresión Lasso o Ridge, ayuda a reducir el impacto del ruido al penalizar modelos excesivamente complejos que podrían ajustarse demasiado a datos ruidosos.
- Aumentación de Datos: particularmente efectiva en problemas de clasificación de imágenes, esta técnica entrena modelos más robustos frente al ruido. Al crear versiones artificialmente ruidosas de las imágenes de entrenamiento, los modelos aprenden a ser más resistentes a la distorsión.
- Técnicas de Preprocesamiento: el preprocesamiento de datos, incluyendo normalización y escalado, contribuye a mitigar el impacto del ruido. Especialmente en redes neuronales, la estandarización de los datos de entrada reduce considerablemente los efectos negativos del ruido aditivo.
Ejemplos Prácticos de Ruido Aditivo
A) En Imágenes
Uno de los contextos donde el ruido aditivo se manifiesta más frecuentemente es en el procesamiento de imágenes. Las imágenes capturadas por diversos sensores, como cámaras digitales, suelen estar contaminadas con ruido debido a factores como baja luminosidad, interferencias electrónicas o limitaciones del hardware.
La adición deliberada de ruido a imágenes puede parecer contraproducente, pero en el contexto de la inteligencia artificial, esta práctica puede aumentar el realismo de las imágenes y hacerlas más vívidas visualmente. Esta técnica resulta particularmente útil en campos como el renderizado 3D, la fotografía digital, la ilustración y la edición fotográfica.
Desde una perspectiva práctica, podemos simular el efecto del ruido aditivo en imágenes utilizando bibliotecas de Python como NumPy y scikit-image:
import numpy as np
import matplotlib.pyplot as plt
from skimage import data, img_as_float
from skimage.util import random_noise
# Cargamos la imagen de ejemplo
image = img_as_float(data.camera())
# Añadimos ruido aditivo gaussiano
noisy_image = random_noise(image, mode='gaussian', var=0.1)
# Mostramos la imagen original y la imagen con ruido
fig, (ax1, ax2) = plt.subplots(1, 2)
ax1.imshow(image, cmap='gray')
ax1.set_title('Imagen original')
ax2.imshow(noisy_image, cmap='gray')
ax2.set_title('Imagen Con Ruido Aditivo Gaussiano')
plt.show()
-----------------------------------------------------------------------------

Este código demuestra cómo introducir ruido gaussiano aditivo a una imagen en escala de grises, permitiendo visualizar tanto la imagen original como la imagen afectada por el ruido.
B) En Señales de Audio
Otro campo donde el ruido aditivo resulta particularmente relevante es el procesamiento de señales de audio. El ruido aditivo deteriora la calidad sonora en comunicaciones, grabaciones y transmisiones de audio. En este contexto, los filtros juegan un papel crucial para eliminar o reducir el impacto de este tipo de ruido.
La técnica de subtracción espectral de potencia es ampliamente reconocida para reducir la presencia indeseada de ruidos en señales de voz. Estudios recientes han investigado su aplicación en señales afectadas por ruido aditivo blanco y colorido, destacando la importancia de disminuir el ruido para preservar la calidad y precisión de la información transmitida por la voz humana[6].
A continuación se muestra un ejemplo en Python que utiliza las bibliotecas NumPy y SciPy para agregar ruido blanco gaussiano a una señal de audio y posteriormente aplicar un filtro para recuperar la señal original:
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import wavfile
from scipy import signal
import requests
import io
# Cargamos el archivo de audio
url = 'https://forodatos.com/multimedia/ruido-aditivo-audio.wav'
response = requests.get(url)
audio_data = io.BytesIO(response.content)
# Leemos el archivo de audio
fs, audio = wavfile.read(audio_data)
# Normalizamos basándonos en el tipo de datos
if audio.dtype == np.int16:
audio = audio.astype(np.float32) / 32768.0
elif audio.dtype == np.int32:
audio = audio.astype(np.float32) / 2147483648.0
# Generamos ruido blanco gaussiano
noise = np.random.normal(0, 0.05, audio.shape)
# Añadimos el ruido aditivo a la señal de audio
noisy_audio = audio + noise
# Aplicamos un filtro para reducir el ruido (Filtro de media móvil)
b, a = signal.butter(5, 0.1, 'low')
filtered_audio = signal.filtfilt(b, a, noisy_audio)
# Visualizamos la señal original, con ruido y filtrada
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(10, 7))
ax1.plot(audio)
ax1.set_title('Señal De Audio Original')
ax2.plot(noisy_audio)
ax2.set_title('Señal De Audio Con Ruido Aditivo')
ax3.plot(filtered_audio)
ax3.set_title('Señal De Audio Filtrada')
plt.tight_layout()
plt.show()
# Guardamos la señal filtrada
if audio.dtype == np.int16:
filtered_audio = np.clip(filtered_audio * 32768, -32768, 32767).astype(np.int16)
elif audio.dtype == np.int32:
filtered_audio = np.clip(filtered_audio * 2147483648, -2147483648, 2147483647).astype(np.int32)
wavfile.write('filtered_audio.wav', fs, filtered_audio)
-----------------------------------------------------------------------------
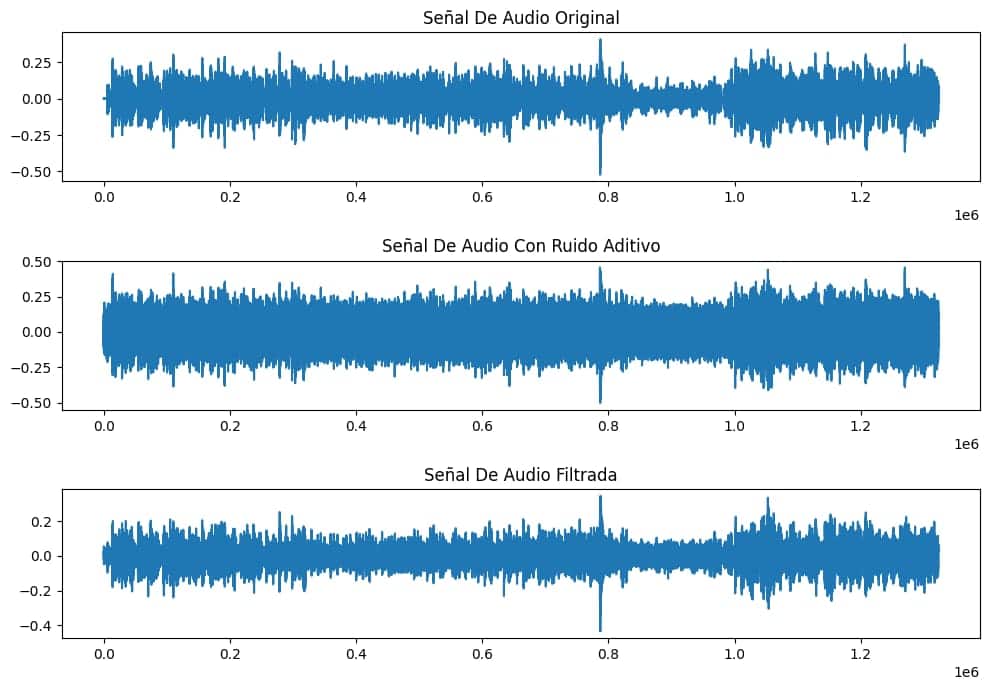
Este código permite visualizar claramente el proceso: la señal original tiene una forma de onda sinusoidal clara, al añadir ruido gaussiano esta señal se distorsiona significativamente, y finalmente el filtro Butterworth pasabajas logra recuperar gran parte de la señal original eliminando las componentes de alta frecuencia del ruido.
C) En Datos de Sensores
Los datos provenientes de sensores suelen estar contaminados con ruido aditivo, afectando la precisión de sistemas de monitoreo y control. Un ejemplo típico es un sensor de temperatura que registra fluctuaciones aleatorias debido a interferencias electromagnéticas o condiciones ambientales adversas.
Podemos simular este escenario y aplicar una técnica de suavizado para mitigar el impacto del ruido:
import numpy as np
import matplotlib.pyplot as plt
# Simulamos los datos de sensor de temperatura con ruido aditivo
np.random.seed(42)
time = np.arange(0, 100, 0.5)
temperature = 25 + 0.5 * np.sin(0.1 * time) # Temperatura real
noise = np.random.normal(0, 0.5, len(time)) # Ruido aditivo gaussiano
temp_with_noise = temperature + noise
# Suavizamos los datos mediante un filtro de media móvil con manejo de bordes
window_size = 5
def moving_average(data, window_size):
weights = np.ones(window_size) / window_size
pad_data = np.pad(data, (window_size/2, window_size/2), mode='edge')
return np.convolve(pad_data, weights, mode='valid')
smoothed_temp = moving_average(temp_with_noise, window_size)
# Visualizamos los datos
plt.figure(figsize=(12, 6))
plt.plot(time, temp_with_noise, label='Temperatura Con Ruido Aditivo', alpha=0.6)
plt.plot(time, smoothed_temp, label='Temperatura Suavizada', linewidth=2, color='orange')
plt.plot(time, temperature, label='Temperatura Real', linestyle='--', color='green')
plt.legend()
plt.xlabel('Tiempo')
plt.ylabel('Temperatura (°C)')
plt.title('Datos De Sensor Con Ruido Aditivo & Suavizado')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
-----------------------------------------------------------------------------
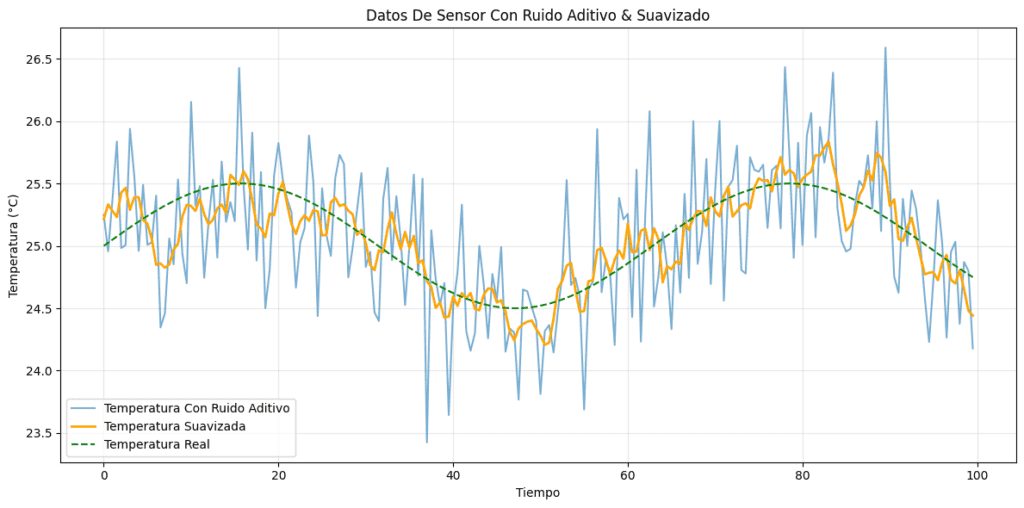
En este ejemplo, el ruido aditivo se modela mediante una distribución gaussiana y se aplica un filtro de media móvil para suavizar la señal, técnica común en sistemas de monitoreo donde las mediciones sensoriales están frecuentemente afectadas por ruido.
Métodos de Mitigación del Ruido Aditivo
Existen diversas técnicas para mitigar el impacto del ruido aditivo, cuya efectividad varía según el contexto de aplicación:
I. Filtración
Los filtros constituyen herramientas fundamentales para eliminar el ruido de las señales, tanto en el dominio temporal como frecuencial:
- Filtro de Butterworth: Filtro analógico o digital diseñado para obtener una respuesta frecuencial lo más plana posible en la banda pasante. Se utiliza habitualmente en procesamiento de señales para eliminar componentes ruidosas de alta frecuencia.
- Filtro de Kalman: Utilizado en aplicaciones que requieren estimar el estado de sistemas dinámicos, este filtro resulta particularmente adecuado para entornos donde tanto la señal como el ruido aditivo evolucionan temporalmente.
Algunas investigaciones han comparado la combinación del filtro de Kalman (tanto en tiempo discreto como en frecuencia) con técnicas de subtracción espectral de potencia para la reducción de ruido en señales de voz contaminadas por ruido colorido. Los resultados sugieren que el filtro de Kalman de tiempo discreto combinado con subtracción espectral ofrece los mejores resultados en términos de distorsión espectral.
II. Reducción de Dimensionalidad
En machine learning, técnicas como el análisis de componentes principales (PCA) ayudan a reducir el ruido en los datos al proyectarlos en espacios de menor dimensión, eliminando así las componentes menos relevantes o más afectadas por ruido.
III. Aumentación de Datos
La aumentación de datos mejora la robustez de los modelos frente al ruido. Para imágenes, por ejemplo, agregar perturbaciones controladas como rotaciones, escalados o ruido ayuda a entrenar modelos más resistentes a la presencia de ruido en datos reales.
La introducción deliberada de ruido durante el entrenamiento de modelos de inteligencia artificial puede parecer contradictoria, pero permite que los modelos aprendan a funcionar con datos imperfectos como los que encontrarán en aplicaciones del mundo real.
IV. Algoritmos Robustos
El desarrollo de algoritmos inherentemente robustos, como modelos de regresión robusta (por ejemplo, Regresión de M-Estimadores), permite que los sistemas sean menos sensibles a datos atípicos o ruidosos. Estos algoritmos resultan particularmente efectivos cuando los datos contienen niveles significativos de ruido aditivo.
Aplicaciones Avanzadas
1. En Telecomunicaciones
En sistemas de telecomunicaciones, el ruido aditivo blanco gaussiano (AWGN) representa un modelo fundamental para analizar el rendimiento de canales de comunicación. La capacidad del canal y la tasa de error están directamente relacionadas con la relación señal-ruido, que cuantifica el nivel de señal deseada respecto al nivel de ruido de fondo.
El filtro adaptado constituye una técnica optimizada para la recepción de señales en presencia de ruido aditivo, maximizando la relación señal-ruido a la salida.
2. En Investigación Avanzada
La investigación actual explora metodologías innovadoras como la segmentación de espectrogramas mediante convolución de modelo-base para detectar señales discretizadas con patrones espectrales específicos contaminadas con ruido aditivo. Estas técnicas resultan prometedoras en campos donde los métodos estándar muestran limitaciones.
Otra línea de investigación interesante involucra la utilización de métodos de linearización local con paso adaptativo para resolver numéricamente ecuaciones diferenciales estocásticas con ruido aditivo, ampliando las aplicaciones a modelos matemáticos complejos.
Conclusión
El ruido aditivo constituye un fenómeno omnipresente en el procesamiento de datos y modelos de aprendizaje automático que, al sumarse directamente a la señal original, degrada potencialmente la calidad de las predicciones y resultados analíticos. Su comprensión resulta crucial para científicos de datos y profesionales de la inteligencia artificial, pues mediante el uso adecuado de técnicas como filtración, regularización, aumentación de datos y algoritmos robustos, pueden diseñarse sistemas que no solo resistan esta interferencia sino que incluso aprovechen su presencia controlada para mejorar el rendimiento en entornos reales, optimizando así la precisión y confiabilidad de las soluciones tecnológicas en campos tan diversos como el procesamiento de imágenes, análisis de señales, telecomunicaciones y sistemas de sensores distribuidos.


